Appendix C
Radiative Corrections
Before measurements of observable quantities can be made in the framework of
the SM, the effects of many secondary effects due to the electromagnetic, weak
and strong interactions must be included.
Such effects are called radiative corrections and naturally divide into three
areas for the general process e+e-® Z0® f[`(f)]) as
follows:
(1) QED Corrections: The corrections due to initial or final state
Bremsstrahlung consisting of those diagrams with an extra photon added as
either a real or virtual photon loop.
The initial state radiative corrections change the center-of-mass energy of
the collision and consequently has a large effect on the line-shape
normalization at LEP.
The final state radiative corrections have a small effect at LEP of
» (3aQ2f)/4p £ 0.17% [99].
(2) Weak Corrections: The corrections due to all other electroweak
diagrams including corrections due to the vector boson propagators g and
Z0, the set of vertex corrections, and box diagrams with two massive boson
exchange [100] [101].
(3) QCD Corrections: The corrections due the final state gluon
radiation which changes the Z0 width by » as/4p = 4% [102].
This appendix presents an overview of the sources of radiative corrections
in the framework of the Standard Model with an emphasis on the electroweak
component (GSW) of the radiative corrections since this specifically applies
to the analysis presented in this thesis.
Since the physical input parameters a, MZ0, MW±,
MH, mf for the SM are clearest in the on-shell scheme where
sin2qW
= 1-[(MW2)/(MZ2)], this scheme will be used in discussing
radiative corrections.
QED Corrections
The QED Corrections are dependent on the details of the experimental setup but
independent of the detailed structure of the underlying non-electromagnetic
part of the theory.
In fact, the only global parameters needed are MZ, GZ, vf, af and
mf, without restriction to the SM.
The corrections have coupling strengths which are determined by the low energy
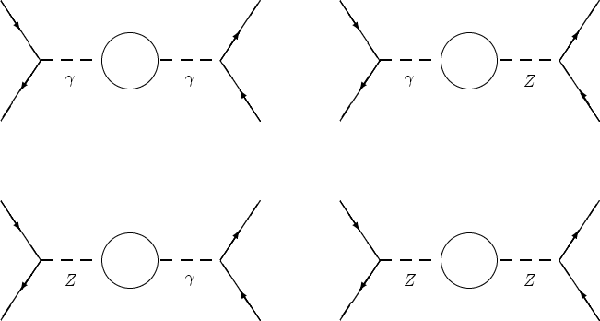
a with the associated O(a) diagrams shown in
Figure C.1.
The corrections are gauge invariant and renormalizable.
At LEP, a realistic treatment of the QED corrections require higher order
contributions than simply O(a).
In general, the practical methods of dealing with higher order QED effects are
broken down into four basic areas:
i) soft photon resummation in the O(a) result,
ii) explicit 2-loop calculations,
iii) the structure function approach, and
iv) the multi-photon radiation according to the method of Yennie,
Frautschi, and Suura (YFS) [63].
The interested reader is referred to references [63] for an excellent
discussion of these higher order QED contributions.
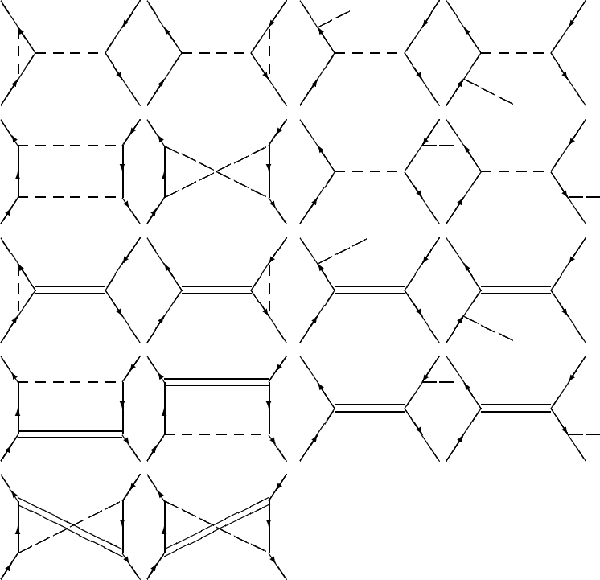
|
Figure C.1: The Feynman Diagrams for O(a) QED Corrections to e+e-® f[`(f)]
Weak Corrections
The Weak Corrections dependent on the detailed internal structure of the theory,
e.g. dependence on the non-Abelian structure and the Higgs sector of the SM,
but are independent of the experimental setup.
In particular, they depend on the unknown parameters MH, mt and therefore
include all the components necessary for the renormalizability of the SM.
Due to the complex structure of the corrections, a detailed treatment of the
corrections is required.
The radiative corrections associated with the weak interaction involve
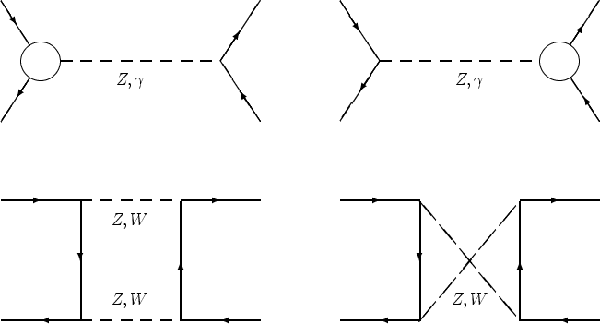
corrections to the vector boson propagators g and Z0 shown in
Figure C.2 [105], corrections to the vertex and
corrections due to the box diagrams with two massive boson exchanged as shown
in Figure C.3 [104], .
In calculating the weak corrections, it is instructive to consider each of the
above corrections separately.
Figure C.2: Propagator Corrections to e+e-® f[`(f)]
Figure C.3: Vertex Corrections and Box Contributions to e+e-® f[`(f)]
Propagator Corrections
The propagator corrections involve all particles in the SM including the
conjectured Higgs boson and top quark, thus depending on MH and mt.
The propagator corrections are implemented in the e+e- amplitude in terms of
three 1PI self-energy functions [105]
The renormalized self-energies are expressed in terms of the non-renormalized
ones as follows [100] [101]:
|
|
| | |
| | |
SgZ(s)- SgZ(0)+ s |
ì
í
î
|
2SgZ(0)
MZ2
|
- |
cos(qW)
sW
|
|
æ
è
|
dMZ2
MZ2
|
- |
dMW2
MW2
|
ö
ø
|
ü
ý
þ
|
|
|
| | |
SZZ(s)- dMZ2 +dZ2Z (s-MZ2) |
|
| | |
SWW(s)- dMW2 +dZ2W (s-MW2) |
|
|
|
| (C.2) |
with
|
|
| | |
-Sgg¢(0)-2 |
cos2(qW)-sin2qW
sinqWcos(qW)
|
|
SgZ(0)
MZ2
|
+ |
cos2(qW)-sin2qW
sin2qW
|
|
æ
è
|
dMZ2
MZ2
|
|
dMW2
MW2
|
ö
ø
|
|
|
| | |
-Sgg¢(0)-2 |
cos(qW)
sW
|
|
SgZ(0)
MZ2
|
+ |
cos2(qW)
sin2qW
|
|
æ
è
|
dMZ2
MZ2
|
|
dMW2
MW2
|
ö
ø
|
|
|
| | |
| | |
|
|
| (C.3) |
with the corrected propagators containing the renormalized 1-particle
irreducible (1PI) one-loop self-energies expressed by [105]:
|
|
| | |
| | |
| | |
| | |
|
|
[s+ |
^
S
|
gg
|
(s)][s-MZ2 + |
^
S
|
ZZ
|
(s)] - |
^
S
|
gZ
|
(s)2 |
|
|
|
|
|
| (C.4) |
The leading terms of the quantity PZ(s) are of the form:
|
|
| | |
-Da+ |
cos2(qW)-sin2qW
sin2qW
|
D |
r
|
+ ··· |
|
|
|
| (C.5) |
where
|
|
| | |
| | |
|
a
4p
|
· |
3
4sin2qWcos2(qW)
|
|
æ
è
|
mt
MZ
|
ö
ø
|
2
|
|
|
|
|
| (C.6) |
where D[`(r)] is identified as the ``r parameter''
[107].
The O(a2) corrected Z0 width, DGZ, is given by,
|
|
| | |
|
å
f
|
NCf |
2
3
|
aMZ
[ vf Re( FVZf (MZ2 )) +af Re( FAZf (MZ2 ))] |
|
| | |
|
å
f
|
NCf |
a
3
|
MZ(vf2+af2) ·dQED |
|
| | |
|
å
f=q
|
NCf |
a
3
|
MZ(vf2+af2) ·dQCD |
|
| | |
|
|
| (C.7) |
together with
|
|
| | |
| | |
|
as(MZ2)
p
|
+ 1.405 |
æ
è
|
as(MZ2)
p
|
ö
ø
|
2
|
|
|
|
|
| (C.8) |
and G(Z® Hf[`(f)]) [108].
Taking into account the mass dependence of the QCD corrections in the partial
width for Z®b[`(b)] increases GZ by 2 MeV with
as(MZ2)=0.11±0.01 [103].
The uncertainty from as induces an uncertainty in the total width of
about ±6 GeV.
The quantities are universal and can be applied to t-channel exchanges as
well.
Photon Exchange
The diagonal g propagator diagram has the following form:
where the real part Re(Pgg(s)) has been absorbed by defining a running
electric charge
.
Z0 Boson Exchange
The diagonal Z0 propagator diagram has the following form:
|
|
| | |
|
e2
4sin2qWcos2(qW)
|
· |
1
1+PZ(s)
|
|
|
| | |
· |
J(e) ·J(f)
|
s-MZ2 + i |
Im( SZ(s))
1+PZ(s)
|
|
|
|
|
|
| (C.10) |
|
|
where
|
|
| | |
|
^
S
|
ZZ
|
(s)- |
|
Re( SZ(s)) = (s-MZ2)PZ(s)
|
|
|
|
| (C.11) |
and the initial (e) and final (f) current matrix elements are given by
|
|
| | |
|
v
|
e
|
[gm (I3e - 2sin2qWQe ) -gmg)5 I3e ] ue |
|
| | |
|
v
|
f
|
[gm (I3f - 2sin2qWQf ) -gmg)5 I3f ] uf |
|
|
|
| (C.12) |
g -Z0 Mixing
The gZ mixing diagram beyond the tree level has following form:
|
|
| | |
gm(vf-afg5 ) + gmQf |
PgZ(s)
1+Pgg(s)
|
|
|
| | |
|
1
2sinqWcos(qW)
|
|
ì
í
î
|
gm
|
é
ë
|
I3f -2Qf |
æ
è
|
sin2qW- sinqWcos(qW) |
PgZ(s)
1+Pgg(s)
|
ö
ø
|
ù
û
|
-I3f gmg5 |
ü
ý
þ
|
|
|
|
|
| (C.13) |
|
|
The redefinition of a universal effective mixing angle, sin2 [`(q)]W, gives
|
|
| | |
sin2 qW- cos(qW)sinqWRe |
æ
è
|
PgZ(s)
1+Pgg(s)
|
ö
ø
|
|
|
| | |
|
|
| (C.14) |
with the fermionic currents expressed in terms of sin2 [`(q)]W,
|
|
| | |
gm(I3e,f - 2Qe,f sin2 |
q
|
W
|
) -I3e,f gmg5. |
|
|
|
| (C.15) |
If the variation of sin2qW is incorporated into the previous formalism, one
obtains,
|
|
|
MW2sin2qW
= MZ2cos2(qW)sin2qW
= |
A
1-Dr
|
|
|
|
|
| (C.16) |
where
|
|
|
A = |
pa
Ö2Gm
|
= ( 37.2802 ±0.0003 GeV )2 |
|
|
|
| (C.17) |
The leading behavior of Dr can be determined by eliminating the
combination e2/ sin2qWcos2(qW) in Equation (C.10) with the help
of Equation (C.16),
|
|
| | |
Da- |
cos2(qW)
sin2qW
|
D |
r
|
+ ··· |
|
|
|
| (C.18) |
and PZ from Equation (C.5) gives,
|
|
|
|
e2
4sin2qWcos2(qW)
|
· |
1
1+PZ(s)
|
|
| | |
| | |
|
|
| (C.19) |
A new quantity, [`(Dr)], is usually defined to relate sin2 [`(q)]W
directly to the Z0 mass:
where the leading terms are given by
where in the light fermion part Da is identical to
Dr.
Vertex Corrections
The vertex corrections refer to the gff and Z0ff 3-point functions
in one-loop order after renormalization with the self-energy contributions to
the external legs included.
In contrast to the propagator corrections
The vertex corrections, unlike the propagator corrections, are not universal,
depending in general on the fermion species.
For this reason, the vertex corrections must be listed separately for n,
e, u, d type fermions (the b quark is exceptional due to the virtual
top contributions in the vertex).
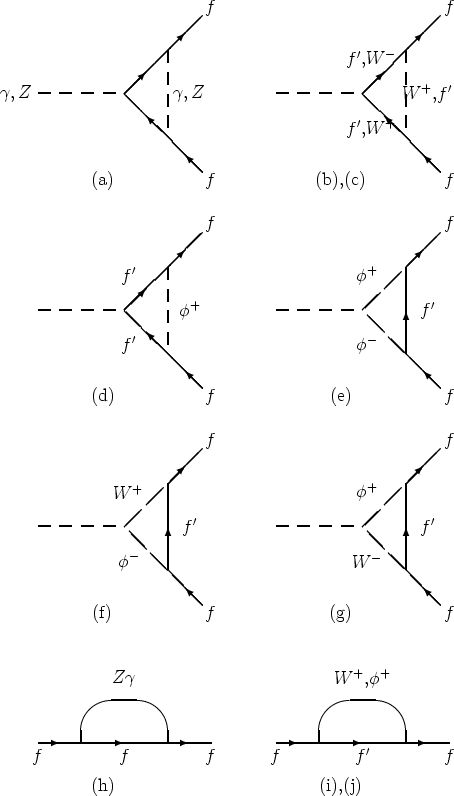
Of the vertex correction diagrams shown in Figure C.3, only
(a)-(c) have non-negligible contributions for f ¹ b, while (d)-(g) are
negligible due to the small Yukawa couplings.
Figure C.4: The Vertex Correction and Fermion Self-energy Interactions
The corrected vertices are given in terms of the weak form factors,
FV,AZ,f and FV,Ag,f for the Zff and gff
vertices as follows [24],
|
|
| | |
iegm(vf -afg5) [ 1+Qf2 FQED(s) ] +iegm
[ FVZf(s) -FAZf(s)g5 ] |
|
| | |
-ieQf gm
[ 1+Qf2 FQED(s) ] -iegm
[ FVgf(s) -FAgf(s)g5 ] |
|
|
|
| (C.22) |
The QED contribution from g exchange is, for Ös >> mf2,
contained in the single form factor
|
|
| | |
|
a
4p
|
-2log |
s
l2
|
|
æ
è
|
log |
s
mf2
|
-1 |
ö
ø
|
+ log |
s
mf2
|
+log2 |
s
mf2
|
+ 4 |
æ
è
|
p2
3
|
-1 |
ö
ø
|
+2pi |
æ
è
|
log |
s
l2
|
- |
3
2
|
ö
ø
|
|
|
|
|
| (C.23) |
where the weak form factors for the neutral current vertices are of the form,
neutrinos:
charged fermions:
|
|
| | |
|
a
4p
|
[ vf (vf2 + 3af2) l2(s,MZ) + FLf ] |
|
| | |
|
a
4p
|
[af (3vf2 + af2) l2(s,MZ) + FLf ] |
|
|
|
| (C.25) |
with
|
|
| | |
|
1
8sin3qWcos(qW)
|
l2(s,MW) - |
3cos(qW)
4sin3qW
|
l3(s,MW) |
|
| | |
- |
8sin3qWcos(qW)
|
l2(s,MW) - |
3cos(qW)
4sin3qW
|
l3(s,MW) |
|
| | |
|
8sin3qWcos(qW)
|
l2(s,MW) - |
3cos(qW)
4sin3qW
|
l3(s,MW) |
|
|
|
| (C.26) |
and the weak form factors for the electromagnetic vertices are of the form,
|
|
| | |
|
a
4p
|
[Qf (vf2 +af2 ) l2(s,MZ) + GLf ] |
|
| | |
|
a
4p
|
[Qf 2vf af l2(s,MZ) + GLf ] |
|
|
|
| (C.27) |
with
|
|
| | |
| | |
- |
1
12sin2qW
|
l3(s,MW) + |
3
4sin2qW
|
l3(s,MW) |
|
| | |
|
1
6sin2qW
|
l3(s,MW) + |
3
4sin2qW
|
l3(s,MW) . |
|
|
|
| (C.28) |
The lengthy expressions for the functions l2, l3, FLb,
and FLb are not listed here but referred to for the readers information
[100] [104].
The infrared divergence are cancelled when the virtual QED corrections are
combined with the corresponding real photon corrections.
Since FQED without real bremsstrahlung is physically meaningless, it is
treated in the more specific discussion of the various measurable quantities
and skipped here.
The values for the leptonic and hadronic form factors for Ös
=MZ2 are
listed in Table C.1 along with the Born coupling constants
ve, ae.
In addition to the contributions from the 2-point functions, the effective
coupling constants near the Z peak are determined by
|
|
|
vf + Re( FVZf (MZ2) ) af + Re( FAZf (MZ2) ) |
|
|
|
| (C.29) |
These effective coupling constants allow an easy estimate of the quantitative
effects in various measurable quantities.
In general, the vertex corrections contribute a correction to the width and
cross-section of the Z0from O(1%) to 4% (in the b case).
Table C.2 lists the effects of the vertex corrections on the
Born cross-section for the processes dG/G(Z®e+e-)
and dG/G(Z®b[`(b)]).
| mt | FVZe(MZ2) | FAZe(MZ2) | vl | al |
| (GeV) | l | l | | |
|
|
| 50 | 0.0019 | 0.0018 | -0.0647 | -0.6005 |
| 100 | 0.0020 | 0.0019 | -0.0778 | -0.6056 |
| 150 | 0.0021 | 0.0020 | -0.0927 | -0.6115 |
| 200 | 0.0021 | 0.0020 | -0.1100 | -0.6191 |
| 250 | 0.0022 | 0.0022 | -0.1244 | -0.6247 |
Table C.1: Leptonic and Hadronic Weak Form Factors
Here MZ
=93 GeV and MH
= 100 GeV.
| mt | dG/G(Z®e+e-) | dG/G(Z®b[`(b)]) |
| (GeV) | % | % |
|
|
| 50 | -0.67 | -0.70 |
| 100 | -0.69 | -1.01 |
| 150 | -0.72 | -1.81 |
| 200 | -0.75 | -2.95 |
| 250 | -0.78 | -3.80 |
Table C.2: Effects of Vertex Corrections
Here MZ
=93 GeV and MH
= 100 GeV.
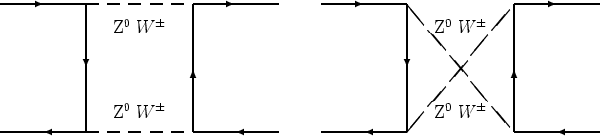
Box Corrections
The electroweak box diagrams include the two gauge boson diagrams as well as the
QED box diagrams.
The contribution of the QED boxes is smaller than that of the gauge boson boxes
due to the cancellations between real and virtual photon contributions to the
phase space.
The weak box diagrams consist of the Z0Z0 and W±W± exchange diagrams
with contributions to the weak amplitude typically of the from
|
|
| | |
e2 |
JNC,CC(e) ·JNC,CC(f)
s
|
· |
a
2p
|
[ I(s,t,MZ) -,+ ±I(s,u,MZ) ] |
|
| | |
e2 |
JNC,CC(e)5 ·JNC,CC(f)5
s
|
· |
a
2p
|
[ +,- ±I5 (s,t,MZ) + I5(s,u,MZ) ] |
|
|
|
| (C.30) |
where
|
|
| | |
|
v
|
e,f
|
gm
(ve,f2 +ae,f2 -2ve,f ae,f g5 ) ue,f |
|
| | |
|
v
|
e
|
gmg5 (ve,f2 +ae,f-2ve,f ae,f g5 ) ue,f |
|
| | |
|
1
4sin2qW
|
|
v
|
e,f
|
gm(1-g5 ) ue,f |
|
|
|
| (C.31) |
The contribution of the gauge boson box diagrams near the Z0 peak is of the
order the a/p to the photon exchange amplitude.
The contribution to the differential cross-section at Ös
= MZ2 is smaller
than 0.02%.
This is because these box diagrams are non-resonant and their contribution
to the Z0 cross-section is suppressed by the large resonance factor.
Improved Born Approximation
As an example of the implementation of radiative effects in the Standard Model,
the cumulative effects of the QED, Weak, and QCD radiative corrections are
presented for the general process e+e-® Z0® f[`(f)].
The approach requires correcting the Born approximation for the process by
including effective values of parameters defining the coupling strengths and
normalizations.
It is sufficient to include the leading light fermion and heavy top
contributions along with the structure suggested from the consideration of
higher orders in the leading terms.
The contributions from the propagators, vertices and boxes are incorporated
through the coupling strengths defined in terms of the original Born parameters
as follows,
|
|
| | |
| | |
| | |
| | |
sin2 |
q
|
W
|
(in J(e) and J(f)) = |
1
2
|
|
æ
ç
è
|
1- |
æ
Ö
|
|
ö
÷
ø
|
|
|
|
|
| (C.32) |
where the r parameter serves as the normalization of the Z0 amplitude
and is given by
|
|
| | |
|
1
1-Dr
|
Dr
= 3 |
Gmmt2
8p2Ö2
|
|
|
|
|
| (C.33) |
and the effective mixing angle parameter, A, is
|
|
| | |
|
pa
Ö2GF
|
º (37.2802±0.0003 GeV)2 |
|
|
|
| (C.34) |
Using these effective parameters, the improved Born invariant amplitude for
e+e-® Z0® f[`(f)] near the Z0 resonance is given by
|
|
| | |
Qe Qf |
4pa(MZ2)
s
|
Jem(e) ·Jem(f) +Ö2GmMZ2r |
|
|
|
|
|
| (C.35) |
where the matrix elements of the electromagnetic current are
|
|
|
Jem(e) = |
v
|
e
|
gmue and Jem(f) = |
u
|
f
|
gmvf |
|
|
|
|
| (C.36) |
or redefined in terms of the effective parameters as
|
|
| | |
( Ö2GmMZ2rf)[ 1/2] |
f
|
gm[I3f (1-g5 ) -2Qf sin2qf] f |
|
|
|
| (C.37) |
The total Z0 width obtained by including the radiative corrections is given
by
|
|
| | |
| | |
NfC |
MZ
12p
|
Ö2GFMZ2r |
Ö
|
1-4mf
|
|
é
ë
|
(If3-2Qfsin2 |
-
q
|
W
|
)2(1+2mf) + (1-4mf) |
ù
û
|
|
|
|
|
| (C.38) |
The improved Born approximation yields values which agree with experimental
results to within 1%, except for the G(Z0® b[`(b)]).
In the case of G(Z0® b[`(b)]), non-leading terms in the vertex corrections,
which are numerically more significant than in the self-energies, give rise to
the deviations from the correct results.
Notice that the improved Born approximation does not contain any information
about the Higgs mass.
More involved treatment of G(Z0® b[`(b)]) as well as other processes with
similar maladies yield closer agreement to experimental results.
In the case of the G(Z0® b[`(b)]),
Additional corrections from the vertex corrections for the G(Z0® b[`(b)])
involving the top quark leads to the modification of the improved Born
approximation parameters r®rb and k® kb
where
|
|
| | |
| | |
sin2 |
q
|
W
|
|
æ
è
|
1+ |
2
3
|
Dr |
ö
ø
|
º sin2 |
q
|
W
|
·kb . |
|
|
|
| (C.39) |
The single Z0b[`(b)] vertex in the Born amplitude is renormalized
by replacing r with
With this parameterization, G(Z0® b[`(b)]) is determined to be 362 MeV, which
agrees with the complete order calculations to within 1% citebib:omicronalphares.